Hidden Speed in CUDA's Shared Memory
In this blog, we’re going to dive into one of the most critical concepts in CUDA programming: shared memory. Shared memory is like the secret ingredient that can supercharge your GPU code. While CUDA’s global memory serves as the main storage, it’s often slow to access repeatedly. That’s where shared memory comes in. It acts as a customizable, fast-access scratchpad where you can store data that is frequently reused by threads within the same block, helping you avoid costly memory transfers. We’ll explore how this works, why it matters, and how you can use it to make your CUDA programs much faster.

CUDA, is almost like the default framework for optimizing code on NVIDIA GPUs with parallelization. It enables us to harness the massive power of GPUs to solve complex problems at incredible speed. Whether it’s deep learning, simulations, or graphics, CUDA allows us to break down large tasks into smaller, manageable chunks and run them simultaneously on thousands of cores. It made NVIDIA, what it is today.
In this blog, we’re going to dive into one of the most critical concepts in CUDA programming: shared memory. Shared memory is like the secret ingredient that can supercharge your GPU code. While CUDA’s global memory serves as the main storage, it’s often slow to access repeatedly. That’s where shared memory comes in. It acts as a customizable, fast-access scratchpad where you can store data that is frequently reused by threads within the same block, helping you avoid costly memory transfers.
Think of it as a private workspace that all the threads in a block can share to optimize performance. We’ll explore how this works, why it matters, and how you can use it to make your CUDA programs much faster. Let’s jump into the magic of shared memory and see how it makes GPU computing even more efficient!
All the code used in this blog can be found here.
Before we discuss the intricacies, intuition and examples of Shared Memory, let us first understand ( revisit ) the basics of CUDA and NVIDIA GPUs Memory Heirarchy.
0. Basics of CUDA
At the core of CUDA programming is a hierarchical model that defines how code is executed in parallel. This model consists of three key components: threads, blocks, and grids.
- Thread: The smallest unit of execution in CUDA, a thread performs the same operation on different data elements in parallel.
- Block: A group of threads that work together. Threads within a block can share data and synchronize their execution through shared memory.
- Grid: A collection of blocks that execute the same kernel function. Each block operates independently, allowing CUDA to manage a vast number of threads efficiently.
To illustrate how these components work together, let’s consider a simple example. Imagine we have an array of 100,000 numbers, and we want to add 1 to each element.The code can be found here.
In a traditional CPU-based approach, this operation would be done sequentially, but with CUDA, we can process the array elements in parallel. Let us first look at how the operation on CPU would look like :
int h_array[ARRAY_SIZE];
for (int i = 0; i < ARRAY_SIZE; i++) {
h_array[i] += 1;
}
This code runs on the CPU, processing each element one by one—an approach that’s inefficient for large datasets. Now, let us do the same operation, but using parallelization on GPU using CUDA.
__global__ void add_one(int *array) {
int idx = blockIdx.x * blockDim.x + threadIdx.x;
if (idx < ARRAY_SIZE) {
array[idx] += 1;
}
}
int main() {
// allocate memory on the device (GPU)
int* d_array;
cudaMalloc(&d_array, ARRAY_SIZE * sizeof(int));
// copy data from host to device
cudaMemcpy(d_array, h_array, ARRAY_SIZE * sizeof(int), cudaMemcpyHostToDevice);
// compute total blocks required
unsigned total_threads = ARRAY_SIZE;
unsigned total_blocks = int(total_threads/BLOCK_SIZE)+1;
// Launch the kernel with 1000 blocks of 128 threads each
add_one<<<total_blocks, BLOCK_SIZE>>>(d_array); // Launching 1000 blocks with 128 threads each
cudaDeviceSynchronize();
// Copy the results back to the host
cudaMemcpy(array, d_array, ARRAY_SIZE * sizeof(int), cudaMemcpyDeviceToHost);
// Free device memory
cudaFree(d_array);
}
The biggest takeaway from this example is how the size of the array is used to compute the required number of thread blocks and how the index of the current thread is computed within the kernel. For more details on the same, please refer to our previous blog on CUDA it Be Any Faster? where we cover the basics of CUDA.
Here are the key points we need to remember in order to understand the conept of shared memory, explained in this blog :
- All threads are divided amongst several thread blocks, where each block contains 1024 threads.
- Each thread block executes independently of each other.
- Each thread block is further divided into warps, with each warp consisting of 32 threads.
- All threads within a warp execute the same intstruction at a given time.
- Two threads in the same thread block but different thread warp may not execute the same instruction at the same time.
1. Basics of CUDA Memory Heirarchy
When data is copied from the CPU to the GPU using cudaMemcpy, it is transferred into the GPU’s RAM, referred to as Global Memory. However, modern NVIDIA GPUs are engineered for high performance and include additional memory components designed to accelerate processing. Beyond just global memory, GPUs feature specialized memory types like Shared Memory, Constant Memory, and Texture Memory, each with unique characteristics that can be leveraged to significantly boost performance. These memory types allow developers to optimize data access patterns, reduce latency, and maximize the computational power of the GPU, making them a critical part of achieving extreme performance in GPU-accelerated applications. Let us look at all these memory components in more detail.
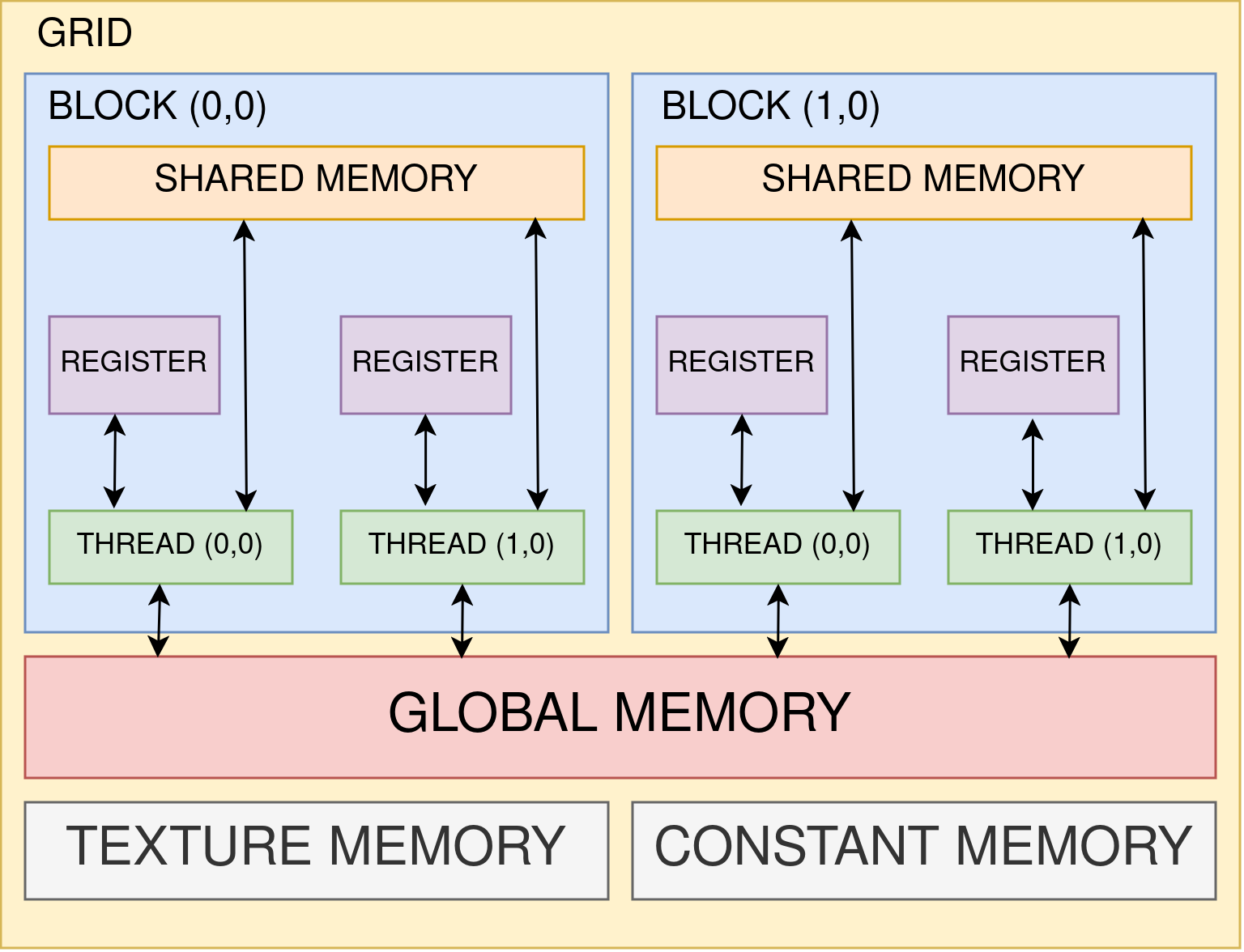
Each thread block in CUDA is allocated its own Shared Memory of size 64KB, which is an on-chip memory accessible by all threads within the block. This shared memory facilitates fast, low-latency communication and data exchange between threads in the same block. Similarly, each individual thread is allocated its own Register, each of size 4 bytes (32 bits), which is an even faster, on-chip storage used for holding temporary variables and performing computations. Registers are private to each thread, ensuring quick access and minimal latency for the thread’s operations. These pieces of information is enough, for the context of learning about leveraging Shared Memory for boosting CUDA performance. We will look at details of these types of memory in a separate blog post.
| Memory Type | Characteristics | Advantages | Trade-offs |
|---|---|---|---|
| Global Memory | - Accessible by all threads across all blocks - Largest memory space on the GPU - High latency (hundreds of clock cycles) - Used for storing data shared among threads or blocks | - Flexibility in accessing large amounts of data | - High latency for frequent access - Requires careful management for data coalescing |
| Constant Memory | - Read-only and cached - Accessible by all threads - Limited size (typically 64KB) | - Fast access for broadcast reads - Suitable for data accessed by all threads | - Small size - Read-only nature limits flexibility |
| Texture Memory | - Read-only and cached - Optimized for spatial locality and supports addressing modes and filtering - Typically used for 2D data | - Efficient for 2D spatial locality - Supports specialized access patterns | - Limited use cases - Overhead for non-2D data access |
| L1/Shared Memory | - On-chip and shared among threads within the same block - Low latency - Limited size (typically 48KB per SM) | - Extremely fast access for intra-block communication - Reduces global memory access | - Limited size - Only accessible within the same block |
2. What is Shared Memory?
At the most granular level in CUDA, we have Threads. These threads are organized into Thread Blocks, and multiple Thread Blocks form a Grid. Now, each Thread Block has its own L1 cache assigned, which is common for all the threads within that block. This L1 cache possesses a unique feature: it is programmable by the user. When the user decides to control what data is stored in this L1 cache ( instead of the GPU driver ), this memory is termed as Shared Memory. The term “Shared” highlights the key aspect of this memory type: the data stored in Shared Memory is accessible to all threads within the same Thread Block. Unlike the traditional cache mechanism, which automatically handles data movement between global memory and L1 cache, shared memory gives programmers direct control over what data is loaded and how it is used.
The design choice behind shared memory stems from the inherent limitations of standard caching. The GPU, while powerful, cannot always predict the best way to utilize cache for specific workloads. It merely attempts to copy contiguous data from global memory to L1 cache and hopes for optimal cache hits. However, real-world applications often require tailored data handling to maximize performance and minimize latency.
This is where shared memory shines. By allowing programmers to explicitly manage the data that gets copied to shared memory, developers can optimize performance for their unique use cases. Shared memory serves as a “scratchpad” memory, where data that is frequently accessed by threads within the same block can be stored and manipulated. In the absence of such a feature, every thread will have to perform read and write to the global memory, which is very expensive. Having frequently accessed and shared data in fast L1 cache reduces the number of costly global memory accesses, which are significantly slower compared to shared memory operations.
In essence, shared memory enables a more efficient collaboration among threads in a block, facilitating faster data sharing and improved performance in parallel computations. Leveraging shared memory effectively can lead to significant performance gains in applications such as image processing, matrix multiplication, and complex simulations, where data reuse and minimizing memory latency are crucial.
Let us understand this with a simple analogy.
3. Chefs making Tomato Soup
Imagine a scenario where multiple chefs are trying to make delicious tomato soup. However, the tomatoes they need are stored in a large fridge located on the ground floor (representing Global Memory). Every time a chef needs a tomato, they have to go down to the ground floor, retrieve the tomatoes, and then return to their kitchen. This process is time-consuming, especially when many chefs are all trying to make their soups simultaneously.

To streamline the cooking process, each kitchen has its own smaller fridge (representing Shared Memory) that is accessible to all the chefs working within that kitchen (Thread Block). Instead of each chef making repeated trips to the ground floor, they can first send one chef to fetch a batch of tomatoes and store them in their shared fridge. Once the tomatoes are in the smaller fridge, all the chefs in that kitchen can easily access them without having to go back and forth to the ground floor.
This setup not only saves time but also enhances collaboration among the chefs in each kitchen. They can quickly share ingredients and coordinate their efforts to create the perfect soup. Just as the chefs benefit from having a shared fridge, threads within a Thread Block benefit from Shared Memory by reducing the time and effort needed to access frequently used data, ultimately leading to more efficient parallel computations in CUDA.
Enough talk, now its show time. It is code time.
4. Matrix Multiplication
Now that we have understood the basics of CUDA, and discussed the concept of Shared Memory, let us stop speaking words, and start writing some code. To that end, we will use Matrix Multiplication in order to understand how Shared Memory can be leveraged. This is how we will go about it.
- Implement Matrix Multiplication on the CPU
- Write a function to perform matrix multiplication using standard nested loops.
- Test the CPU implementation for correctness and performance.
- Implement a Naive CUDA Kernel for Matrix Multiplication on the GPU
- Write a basic CUDA kernel to perform matrix multiplication.
- Allocate memory for matrices on the GPU and transfer data from the host to the device.
- Launch the CUDA kernel and retrieve the result back to the host for verification.
- Optimize Using Shared Memory
- Modify the CUDA kernel to utilize shared memory.
- Test the optimized kernel for correctness and compare performance with the naive implementation.
4.1 Matmul on CPU : Slow and Steady
In this section we will discuss how Matmul can be performed on the CPU with 3 nested for loops. This is the slowest way with zero parallelization, and will hence act as the benchmark. The code can be found here.
Let us take two 4x4 matrices A and B multiplied to give another 4x4 matrix C as shown in the figure below. Each element from the ith row of A is multiplied with each element of the jth column of B, and summed up to give the element (i,j) of C.
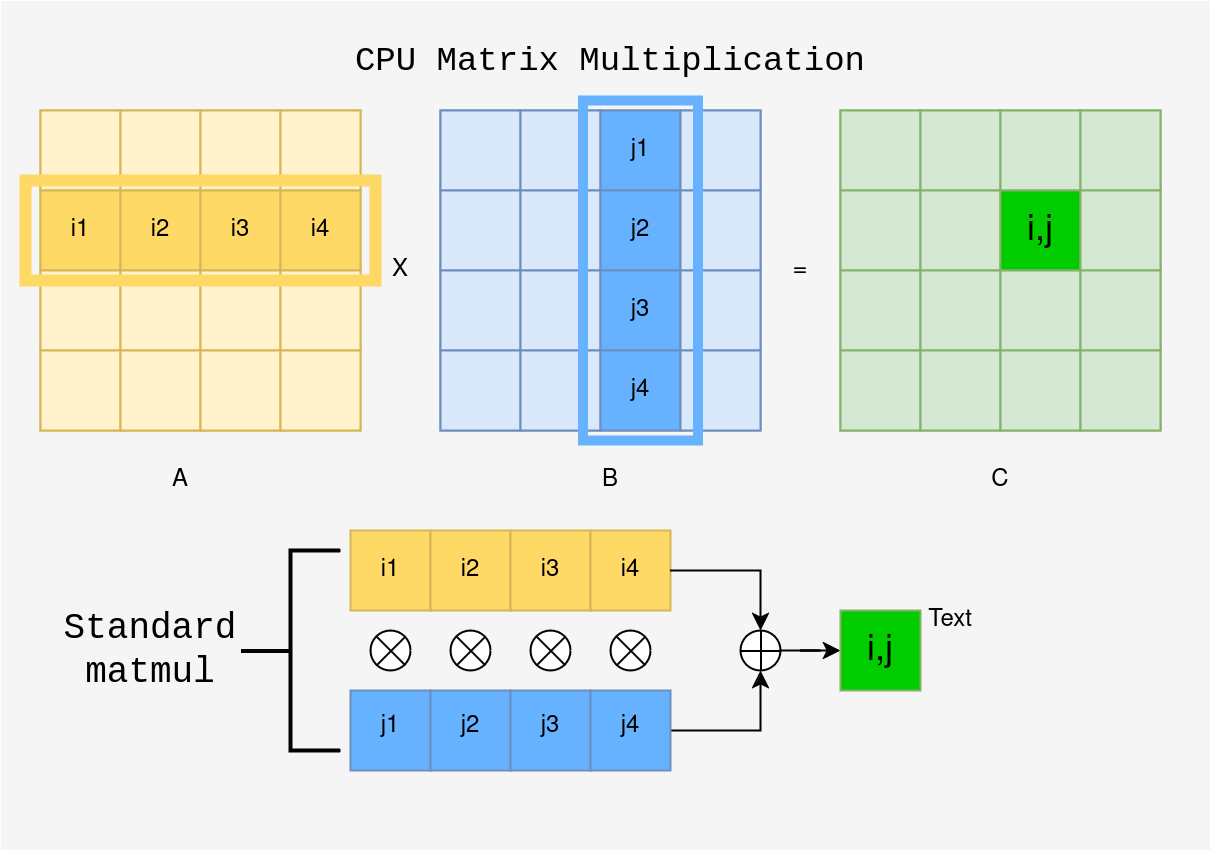
void matmul_cpu(const std::vector<float>& A, const std::vector<float>& B, std::vector<float>& C, int n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
float sum = 0.0f;
for (int k = 0; k < n; k++) {
sum += A[i * n + k] * B[k * n + j];
}
C[i * n + j] = sum;
}
}
}
When we use this function for multiplying two square matrices of size (1024x1024), and measure the latency :
Average CPU Time: 582.865ms
Thats more than half a second for a single matmul operation. We can definitely do better. Let us now look at a simple CUDA kernel and see how fast a naive implementation can get.
4.2 Matmul on GPU : The CUDA way.
The matmul_cuda_naive CUDA kernel performs matrix multiplication for two square matrices A and B, storing the result in matrix C. Each thread computes its unique row and column indices based on its block and thread identifiers, ensuring it operates within the bounds of the matrices. For each valid thread, the kernel initializes a sum variable and performs the dot product by iterating through the elements of the respective row of A and column of B. Finally, it stores the computed sum in the corresponding position of matrix C. The code can be found here.
__global__ void matmul_cuda_naive(float* A, float* B, float* C, int n) {
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
if (row < n && col < n) {
float sum = 0.0f;
for (int k = 0; k < n; k++) {
sum += A[row * n + k] * B[k * n + col];
}
C[row * n + col] = sum;
}
}
On using this kernel for matrix multiplication of the same (1024x1024) matrices, we obtain :
Average CUDA Naive Time: 2.42381ms
The CUDA matrix multiplocation is 240.19x times faster than the CPU version. This is already pretty mind blowing, one might argue. Lets put 240x times in perspective. If the matmul on GPU took a minute, the same operation on the CPU would take 4 hours to complete.
Not fast enough? Cool. Then lets make it even faster by using (no prize for guessing) SHARED MEMORY.
5. Matrix Multiplication with Shared Memory
In this section, we will explore how Shared Memory can enhance the efficiency of Matrix Multiplication. The approach we will adopt may seem counterintuitive and could be challenging to grasp initially. Therefore, we will begin by examining the multiplication of smaller matrices, specifically the same 4x4 matrix example, using a block size of 2x2. This simplified example will provide a solid foundation, making it easier to comprehend the implementation for larger matrices later on.
5.1 Intuition of using Tiled Matmul.
As shown below, matrix multiplication can be done in parts, where sub-blocks (i1, i2) from matrix A and (j1, j3) from matrix B are multiplied to compute the partial result of element C(i,j). The process is repeated for (i3, i4) and (j2, j4) to complete the sum for C(i,j). In summary, instead of computing all the multiplications and summing them at once, we split the work into two steps.
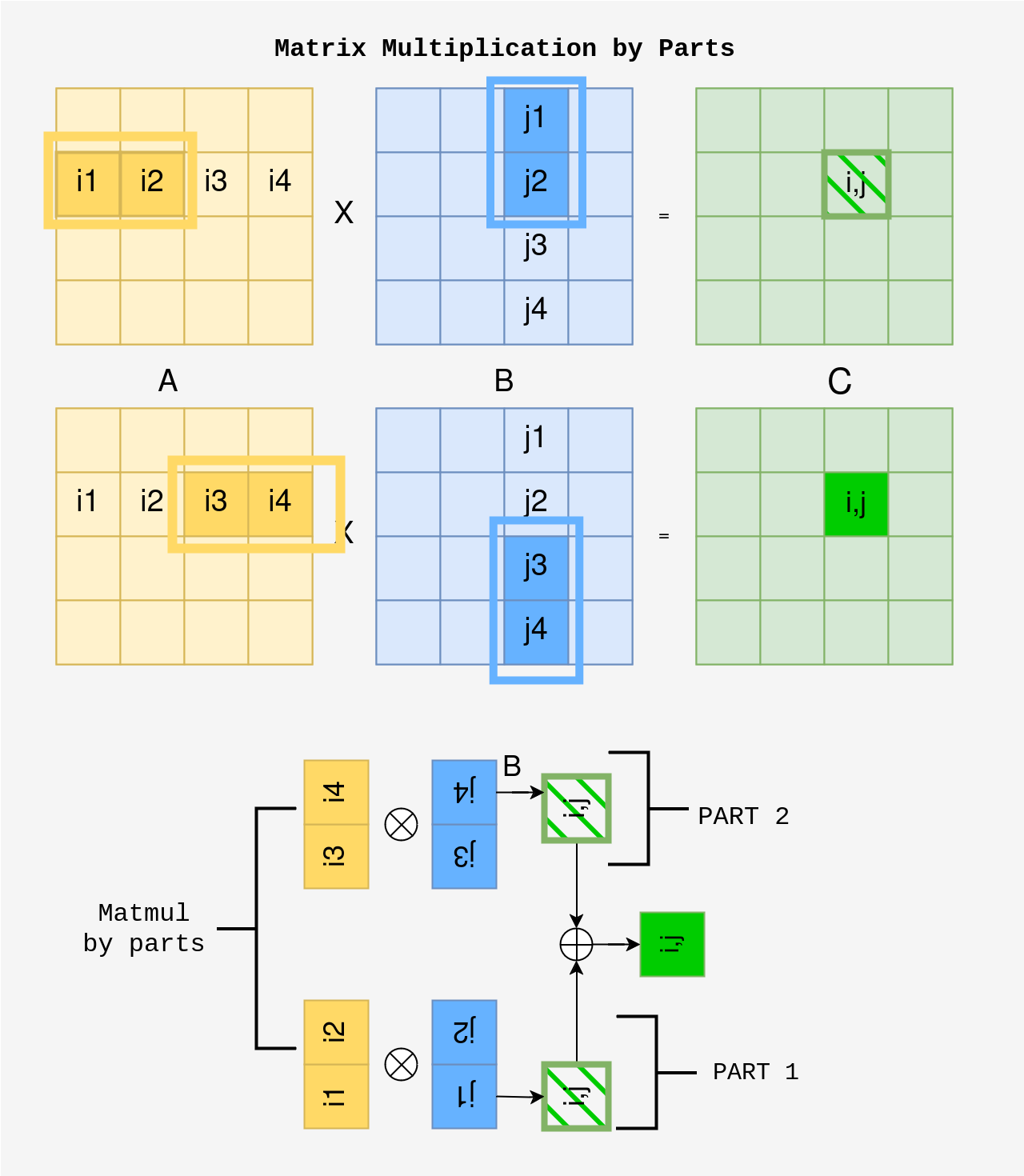
This intuition can be extended to help understand Tiled Matrix Multiplication. Instead of computing the matrix multiplication for the entire 4x4 matrix at once, we can break it down and compute the multiplication for each 2x2 block separately.
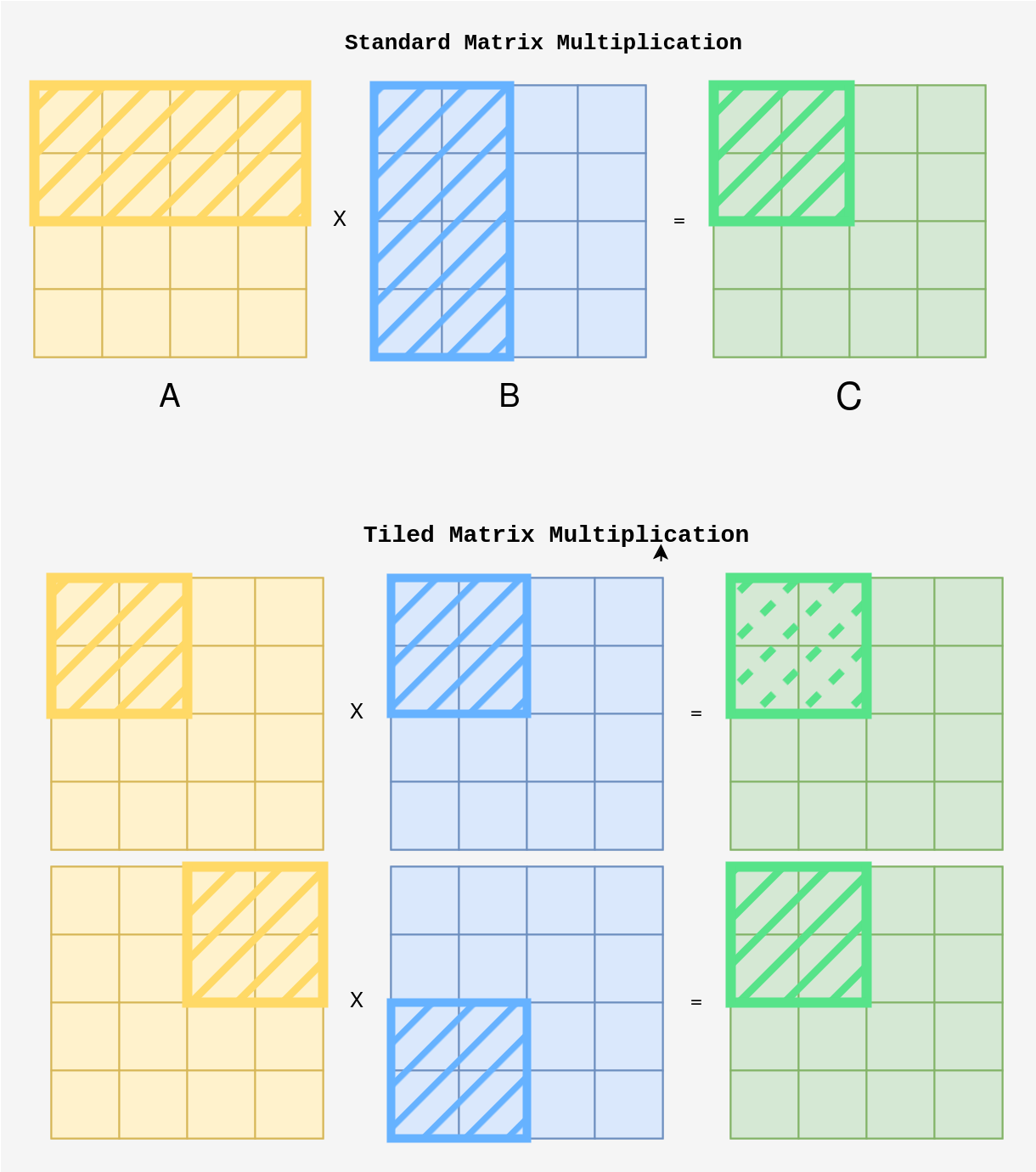
As shown above, when computing each 2x2 block in matrix C, we can first calculate the matrix multiplication for the first 2x2 block in matrices A and B. After that, we move on to the next 2x2 block and compute its contribution. By summing these partial results, we gradually build the final result for the entire matrix.
This tiled approach allows us to handle smaller chunks of the matrices at a time, making it more efficient by utilizing faster memory (like shared memory) to perform intermediate computations.
5.2 Tiled Matmul with Shared Memory in CUDA
In this approach, we use shared memory to speed up the multiplication by working on small parts (tiles) of the matrices at a time. We already looked at how Tiled Matmul works for the 4x4 matrix as shown in the diagram above. Lets use the same example to understand how shared memory can be leveraged with Tiled Matrix Multiplication.
- Assigning Threads: For a matrix of size 4x4, we use
16 threads, one for each element in the outputmatrix C. Each thread will be responsible for calculating one element of matrix C.
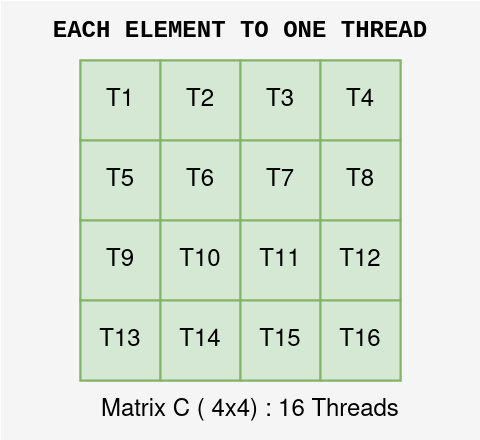
-
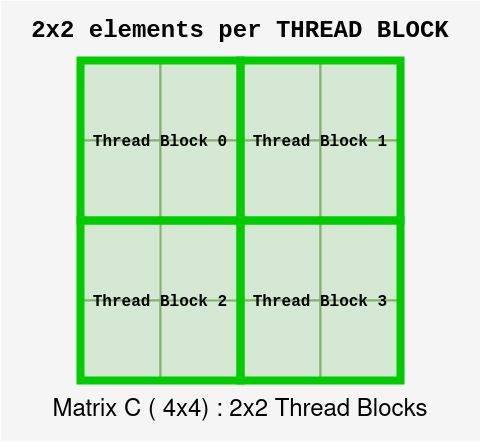
Breaking into Tiles: Instead of multiplying the entire matrix at once, we break it down into smaller 2x2 tiles. Each tile represents a section of the matrix, and this makes the problem easier to handle in smaller chunks.
-
Thread Block Assignment: Each
2x2 tilefrom the resultmatrix Cis assigned to a thread block. The threads within that block are responsible for computing the values of this 2x2 section by multiplying corresponding 2x2 tiles from matricesAandB.
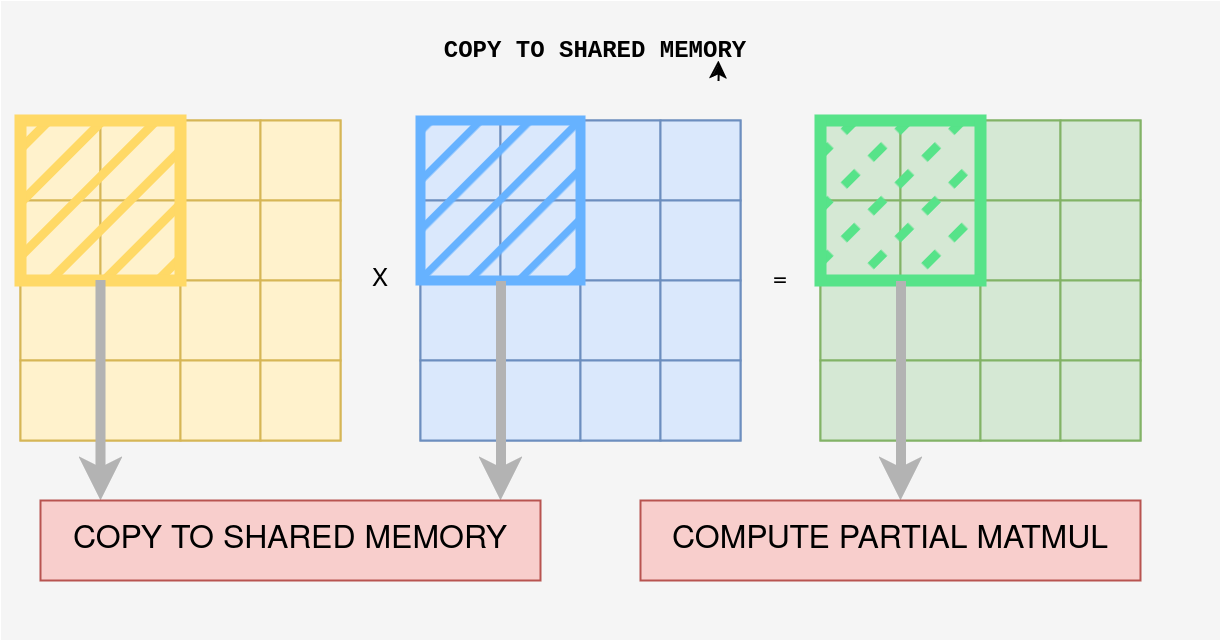
- Loading Data into Shared Memory: For each tile in matrix
C, we first load the corresponding2x2 tilesfrom matricesAandBinto shared memory. Shared memory is fast and allows threads to access the required data quickly, avoiding the slower global memory.
-
Synchronizing Threads: Once all the threads have loaded their part of
AandBinto shared memory, we synchronize the threads so that everyone is ready to use the data at the same time. -
Performing the Partial Multiplication: : The threads in the block perform the matrix multiplication for this tile, using the data stored in shared memory. Each thread computes a partial result by multiplying corresponding elements from the current tile of A and B (just like we mentioned earlier: i1 * j1 + i2 * j2).
-
Repeat for Other Threads: After computing the first set of
2x2 tiles, we move on to the next tiles fromAandB, repeating the process until all partial results for the tile inCare summed up. -
Accumulating Results: The thread adds these partial results together. After processing all tiles, the full result for each element of
Cis accumulated. -
Writing Back to Global Memory: Once all threads are done with their computations, the final values for matrix C are written back to global memory.
In summary, when performing matrix multiplication using shared memory in CUDA, we first copy the necessary data for each thread block’s 2x2 tile into shared memory and then write the results back to global memory after the computation is complete.
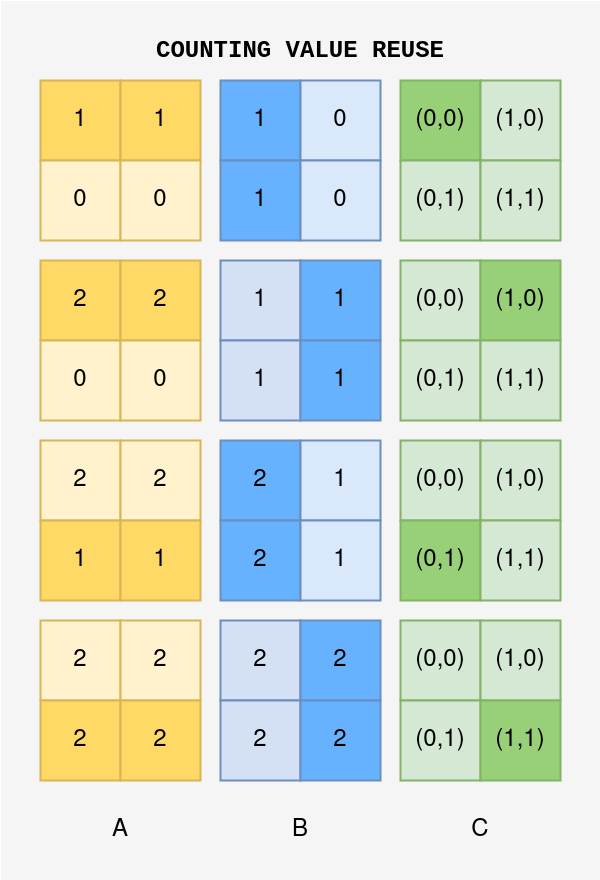
5.3 Reusing Data from Shared Memory
A key advantage of this approach is the efficient reuse of data. For every 2x2 tile in the result matrix C, each element from the corresponding tiles in A and B is reused twice. This reuse reduces the need for multiple accesses to global memory, as the values are already stored in shared memory after the initial copy. By reducing redundant memory accesses, we significantly improve the performance of the matrix multiplication process. The diagram you provided illustrates how the values in the blue and yellow grids are reused during each step of the multiplication.
5.4 Talk is Cheap. Show me the Code.
We’ve discussed a toy example of multiplying two 4x4 matrices using 2x2 tile using shared memory to improve performance. In this section, we’ll look at the code, and extend the same concept, where the grid is divided into 32x32 blocks, each handled by a block of threads, and the computation for each element in the output matrix is handled by the respective threads in the block. The code can be found here.
Let’s dive into the code, which is essentially the same but operates on larger tiles (32x32).
#define BLOCK_SIZE 32
__global__ void matmul_cuda_shared(float* A, float* B, float* C, int n) {
// define A and B sub matrices of size 32x32 in shared memory.
__shared__ float Asub[BLOCK_SIZE][BLOCK_SIZE];
__shared__ float Bsub[BLOCK_SIZE][BLOCK_SIZE];
// get global x and y indices for this thread and block.
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
// variable to store sum ( stored on registers )
float sum = 0.0f;
// iterate over all tiles for this thread block.
for (int blockIdx = 0; blockIdx < (n + BLOCK_SIZE - 1) / BLOCK_SIZE; blockIdx++) {
// Load tiles into shared memory
if (row < n && blockIdx * BLOCK_SIZE + threadIdx.x < n)
Asub[threadIdx.y][threadIdx.x] = A[row * n + blockIdx * BLOCK_SIZE + threadIdx.x];
else
Asub[threadIdx.y][threadIdx.x] = 0.0;
if (col < n && blockIdx * BLOCK_SIZE + threadIdx.y < n)
Bsub[threadIdx.y][threadIdx.x] = B[(blockIdx * BLOCK_SIZE + threadIdx.y) * n + col];
else
Bsub[threadIdx.y][threadIdx.x] = 0.0;
// Synchronize to make sure all the data is copied to shared memory.
__syncthreads();
// Compute matrix multiplication for the tile
for (int k = 0; k < BLOCK_SIZE; k++) {
sum += Asub[threadIdx.y][k] * Bsub[k][threadIdx.x];
}
__syncthreads();
}
// Copy the data to global memory.
if (row < n && col < n) {
C[row * n + col] = sum;
}
}
Now, let’s break this down step by step.
-
Block Size and Shared Memory: The
BLOCK_SIZEis set to32, meaning each thread block handles a32x32 tile. Shared memory is allocated for storing sub-matrices (tiles) from matrixAand matrixBin Asub and Bsub. The__shared__keyword is key here—it allocates memory for all threads within a block to share during the computation, avoiding slower global memory accesses.// define A and B sub matrices of size 32x32 in shared memory. __shared__ float Asub[BLOCK_SIZE][BLOCK_SIZE]; __shared__ float Bsub[BLOCK_SIZE][BLOCK_SIZE]; - Mapping Threads to Tiles: Each thread in a block is responsible for calculating
one elementin a32x32tile of the result matrixC. The thread’s position in the block corresponds to a specificrowandcolumnwithin the tile.// get global x and y indices for this thread and block. int row = blockIdx.y * blockDim.y + threadIdx.y; int col = blockIdx.x * blockDim.x + threadIdx.x; -
Loading Tiles into Shared Memory: In the loop, tiles from matrices
AandBare loaded into shared memory. Each thread copies one element from the global memory (the larger matricesAandB) into the shared memory tiles (AsubandBsub). This process is repeated for multiple tiles as we move across the matrices.// Load tiles into shared memory if (row < n && blockIdx * BLOCK_SIZE + threadIdx.x < n) Asub[threadIdx.y][threadIdx.x] = A[row * n + blockIdx * BLOCK_SIZE + threadIdx.x]; else Asub[threadIdx.y][threadIdx.x] = 0.0; if (col < n && blockIdx * BLOCK_SIZE + threadIdx.y < n) Bsub[threadIdx.y][threadIdx.x] = B[(blockIdx * BLOCK_SIZE + threadIdx.y) * n + col]; else Bsub[threadIdx.y][threadIdx.x] = 0.0; - Synchronization: After copying data into shared memory,
__syncthreads()is called. This ensures that all threads in the block have completed copying their respective elements before moving on to the computation. Synchronization is crucial here because shared memory is used by all threads in the block, and we don’t want any thread to start using data that hasn’t been fully copied.// Synchronize to make sure all the data is copied to shared memory. __syncthreads(); - Computing the Tile: After loading a tile into shared memory, each thread computes part of the matrix multiplication for that tile. For a given row in
Aand column inB, the corresponding thread will compute the dot product, accumulating the result insum.// Compute matrix multiplication for the tile for (int k = 0; k < BLOCK_SIZE; k++) { sum += Asub[threadIdx.y][k] * Bsub[k][threadIdx.x]; } __syncthreads(); - Writing Back to Global Memory: Once the partial product for the tile is calculated, the results are written back to global memory in the matrix
C. This is done after all tiles have been processed and summed.// Copy the data to global memory. if (row < n && col < n) { C[row * n + col] = sum; }
This code shows how to extend the concept of tiled matrix multiplication to larger blocks (32x32) using shared memory. The basic steps involve:
- Copying the required sub-matrices (tiles) from global memory into shared memory for fast access.
- Performing matrix multiplication within each block using the shared tiles.
- Storing the final results back into global memory.
By making effective use of shared memory, we minimize the number of slow global memory accesses, which results in significantly faster matrix multiplication.
In essence, the shared memory acts as a cache for data reuse within the block. For example, each value in a tile of A and B is reused 32 times during the matrix multiplication. Without shared memory, the same value would need to be loaded from global memory repeatedly, slowing down the computation.
Let us now compare the time improvement due to Shared Memory.
Average CPU Time: 568.871ms
Average CUDA Naive Time: 2.42451ms
Average CUDA Shared Memory Time: 1.91292ms
By using shared memory, this time is further reduced to 1.91292 ms, providing about a 1.27x speedup compared to the naive CUDA approach. This speedup comes from the efficient reuse of data within shared memory, which avoids multiple global memory accesses and significantly enhances computation speed, showcasing the advantage of shared memory in optimizing matrix multiplication.
6. Summary
In this blog, we explored how shared memory can significantly boost the performance of CUDA programs by reducing the need for repetitive data transfers from global memory. We started by understanding the basics of thread and block organization in CUDA, and then introduced the concept of shared memory as a customizable and high-speed alternative to the default memory hierarchy. By storing frequently accessed data in shared memory, we enable threads within a block to reuse it efficiently, avoiding costly memory fetches.
We looked at an example of matrix multiplication using the Tiled Matmul technique, where we saw how shared memory allows us to load, compute, and reuse data efficiently. With shared memory, each thread in a block can access the data needed for computations directly from a faster, local cache rather than repeatedly querying global memory.
Ultimately, shared memory gives programmers more control over what data gets cached, leading to a dramatic reduction in memory latency and an overall performance boost, as seen in the 2x speedup in our example. With these concepts in mind, you’re now equipped to start leveraging shared memory in your own CUDA programs for optimized performance!
Enjoy Reading This Article?
Here are some more articles you might like to read next: