FlashAttention in CUDA

A CUDA C++ reimplementation of FlashAttention fusing QK⊤, softmax, and PV into a single kernel. Tiles of queries, keys, and values are stored in shared memory and registers, while a numerically stable online softmax is computed incrementally. This eliminates the need for the full N×N attention matrix in GPU memory, drastically reducing HBM I/O. The result is a 3.05× speedup over a naïve three-kernel baseline, transforming self-attention from memory-bound to compute-bound.

Github Link : https://github.com/sanket-pixel/flash_attention

Summary of Flash Attention

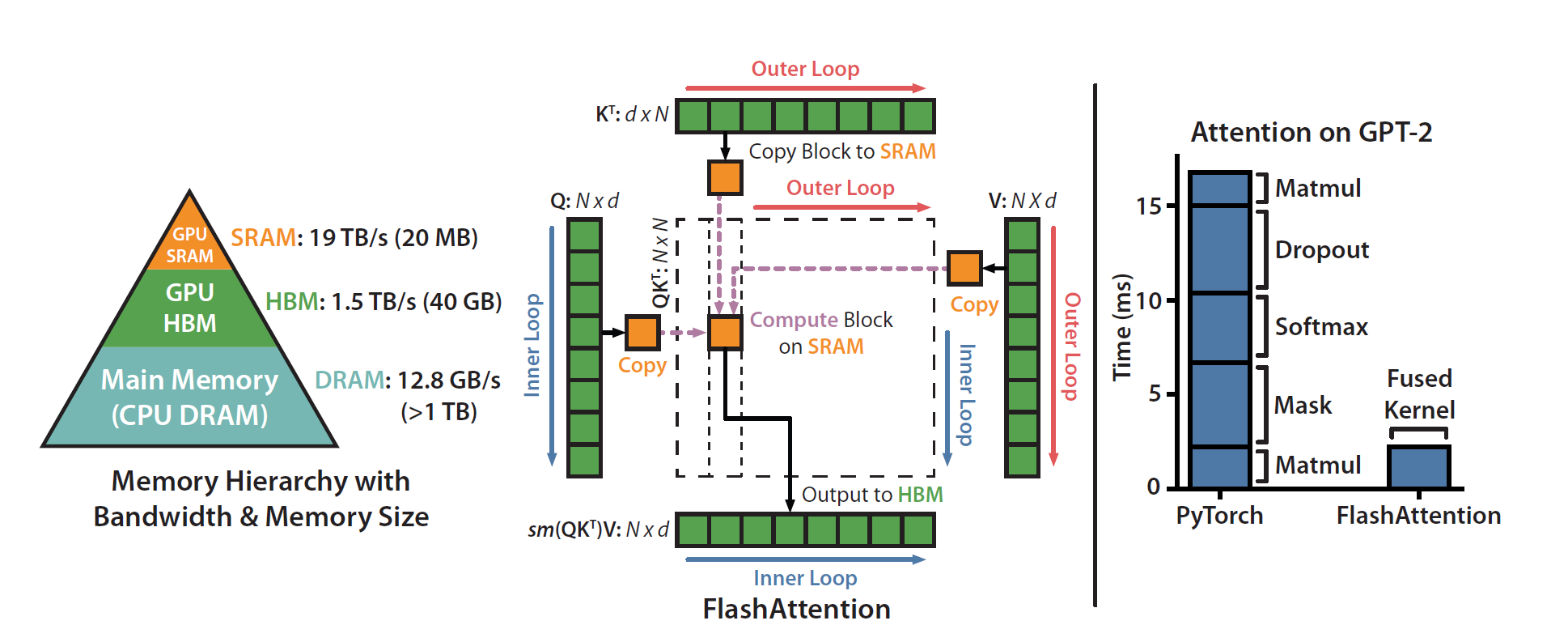
1. Why Standard Self-Attention is a Memory Bottleneck

Self-attention (the core of Transformer blocks) is defined as:

where:

• Q ∈ ℝ^{N × d_k}
• K ∈ ℝ^{N × d_k}
• V ∈ ℝ^{N × d_v}
• N — sequence length
• d_k — head dimension

A direct (naïve) implementation computes the score matrix:

For realistic N (e.g., N = 4096) this matrix alone is enormous: N^2 = 16,777,216 elements.
The practical issue is not FLOPs but HBM (GPU DRAM) traffic.

• The baseline pipeline writes S to global memory, then reads S for softmax, writes P = softmax(S), then reads P to compute O = PV. That produces several expensive global memory round-trips.
• Thus runtime becomes memory-bound with O(N^2) memory I/O dominating execution, while GPU ALUs sit underutilized.

The aim of FlashAttention-style implementations is to avoid materializing the full (NxN) matrix, turning the workload from memory-bound to compute-bound by using on-chip storage and streaming tiles.

2. The Baseline Implementation

A straightforward CUDA implementation splits attention into three kernels:

1. Scores: S = Q K^\top (tiled GEMM).
2. Softmax: P = softmax(S) (row-wise softmax).
3. Output: O = P V (tiled GEMM).

void attention_cuda_kernels_only(float *dQ, float *dK_t, float *dV, float *dO,
                                 float *dS_buffer, float *dP_buffer, int n,
                                 int dim) {
  int num_blocks_N = (n + BLOCKSIZE - 1) / BLOCKSIZE;
  int num_blocks_d = (dim + BLOCKSIZE - 1) / BLOCKSIZE;

  // S = Q.K_t 
  dim3 grid_dim_qk(num_blocks_N, num_blocks_N, 1);
  dim3 block_dim_qk(BLOCKSIZE, BLOCKSIZE, 1);
  tiled_matmul<<<grid_dim_qk, block_dim_qk>>>(dQ, dK_t, dS_buffer, n, dim, n);

  // P = softmax(S)
  dim3 grid_dim_p(num_blocks_N, 1, 1);
  dim3 block_dim_p(BLOCKSIZE, 1, 1);
  softmax_cuda<<<grid_dim_p, block_dim_p>>>(dS_buffer, dP_buffer, n);

  // O = PV
  dim3 grid_dim_pv(num_blocks_d, num_blocks_N, 1);
  dim3 block_dim_pv(BLOCKSIZE, BLOCKSIZE, 1);
  tiled_matmul<<<grid_dim_pv, block_dim_pv>>>(dP_buffer, dV, dO, n, n, dim);
}

Problems with this approach:

• S and P are very large and are written to and read from HBM multiple times.
• Each kernel launch incurs overhead and requires reading/writing large intermediate buffers.
• Even tiled GEMMs cannot overcome the repeated global memory traffic for those intermediate matrices.

3. FlashAttention

Core insight: never materialize the full (NxN) attention matrix in global memory and compute the effects of each block of keys/values on the outputs on the fly.

Key techniques used in the single fused kernel:

• Kernel fusion: Compute Q.K, the softmax normalization, and the final matrix-vector accumulation P.V within one kernel, avoiding intermediate global writes.
• Tiling & shared memory: Stream tiles (e.g., 32×32 blocks) of K and V into __shared__ memory and reuse them for multiple Q rows.
• Online (incremental) softmax: Maintain running max and running (unnormalized) sum per query row so you never need all scores simultaneously.
• Warp-level intrinsics: Use __shfl_down_sync and __shfl_sync for low-latency warp reductions (max and sum) without extra __shared__ reductions or global syncs.
• Register/shared accumulation of O: Accumulate the partial PV contributions tile-by-tile, updating the output in a numerically stable, incremental way.

Together, these techniques reduce HBM I/O from O(N^2) intermediate traffic to streaming inputs + writing outputs, i.e., roughly O(N.d) global transfers which is a massive reduction.

4. Deep Dive into the flash_attention Kernel

The flash_attention CUDA kernel implements a memory-efficient version of self-attention by fusing multiple steps and avoiding the explicit materialization of the N \times N attention matrix. The key idea is to operate on tiles of Q, K, and V in GPU on-chip shared memory (__shared__) while performing an online, numerically stable softmax.

4.1. Shared Memory Tiling

• Qi[32][d] stores a tile of Q for the current block of queries.
• Kj[d][32] stores a tile of K for the corresponding block of keys.
• Vj[32][33] stores the associated values V.

These tiles are loaded from global HBM in a coalesced fashion, significantly reducing high-latency memory accesses:

for (int c = 0; c < iter_x_Q; c++) {
    Qi[threadIdx.y][c * blockDim.x + threadIdx.x] =
        Q[(blockIdx.y * blockDim.y + threadIdx.y) * dim +
          (c * blockDim.x + threadIdx.x)];
}
__syncthreads();

4.2. Iterating Over Key-Value Tiles

The kernel loops over Tc = N / Bc tiles of keys and values (Bc = 32). For each tile:

• A sub-block of K and V is loaded into shared memory.
• Each thread computes the dot product of its query row with the key column, forming partial attention scores:

float s_value = 0;
for (int m = 0; m < dim; m++) {
    s_value += Qi[threadIdx.y][m] * Kj[m][threadIdx.x];
}

4.3. Online Softmax Computation

Rather than storing the full attention scores, the kernel uses a running maximum (m_i) and sum of exponentials (l_i) to compute the softmax in a numerically stable manner:

The normalized softmax value is then applied incrementally to the output:

Warp-level reductions using __shfl_down_sync and __shfl_sync efficiently compute m_{ij} and l_{ij} across threads without additional shared memory:

unsigned int delta = 16;
while (delta >= 1) {
    float value_from_partner =
        __shfl_down_sync(0xffffffff, thread_level_max, delta);
    thread_level_max = max(thread_level_max, value_from_partner);
    delta = delta / 2;
}
float m_ij = __shfl_sync(0xffffffff, thread_level_max, 0);

4.4. Output Accumulation

For each query, the weighted sum over the value vectors is computed incrementally using the updated softmax normalization:

o_i = (1 / li_new) *
      (li * exp(mi - mi_new) * o_i + exp(m_ij - mi_new) * o_acc_partial);

After all key-value tiles are processed, the final attention output for each query is stored in global memory:

4.5. Key Takeaways

• Memory-Bound → Compute-Bound: By avoiding the full N \times N attention matrix in HBM, the kernel drastically reduces GPU memory traffic.
• Shared Memory Efficiency: Tiling leverages fast on-chip memory to accelerate the computation.
• Numerical Stability: The online softmax algorithm maintains correctness for large N without precision loss.
• Warp-Level Parallelism: __shfl_* primitives eliminate the need for global reductions, maximizing throughput.

This design allows large-scale attention operations (e.g., N = 4096) to execute efficiently on GPU, achieving a significant speedup compared to the naive baseline.

5. Performance Results and Conclusion

Benchmark setup in the provided host code: N = 4096, d = 64, BLOCKSIZE = 32, averaged over BENCHMARK_RUNS = 20.

(speedup = 21.8565 / 7.1659 ≈ 3.05)

Why this speedup occurs

• HBM I/O reduced: The baseline materializes (S) and (P) and reads/writes them to/from HBM multiple times → (\mathcal{O}(N^2)) memory traffic.
• FlashAttention streams tiles: Only inputs Q,K,V and outputs O touch global memory; tile internals live in registers/__shared__ → far less global traffic (roughly (\mathcal{O}(N\cdot d)) transfers).
• Compute-bound execution: With minimized memory stalls, the GPU spends proportionally more time on arithmetic (higher ALU utilization), thus running faster.

6. Notes, caveats & possible improvements

• Assumptions in the code: The kernel expects n and d to be multiples of tile sizes (BLOCKSIZE, etc.). Real code should handle remainders safely.
• Shared memory layout & bank conflicts: Vj is declared 32×33 (an extra column) likely to avoid bank conflicts or to align to 128B boundaries — this is a common technique and should be annotated in production code.
• Numerical precision: The code uses float. Mixed-precision (FP16/BF16) with careful accumulation can further improve throughput on modern GPUs (Tensor Cores), but requires extra care with numerical stability.
• Multi-head & batched attention: Extending this kernel to multi-head, variable-length sequences, or batching will require loop reorganization and additional indexing logic.
• Tensor Cores & WMMA: A production implementation leveraging tensor cores (WMMA) and cooperative groups can further increase throughput for d that align with Tensor Core shapes.

7. Conclusion

This single-file CUDA implementation of FlashAttention demonstrates the key idea of I/O-aware GPU programming: algorithmic performance is often limited by memory movement, not arithmetic. By fusing kernels, tiling inputs into __shared__ memory, and using a numerically stable online softmax, the implementation reduces HBM traffic and turns a memory-bound attention computation into a compute-bound one leading to a 3.05× empirical speedup on the provided benchmark.